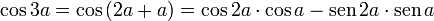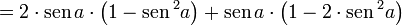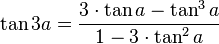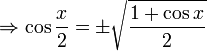Curiosidades de Matemática
Pesquisar este blog
domingo, 27 de fevereiro de 2011
Pressão Sanguínea
Ao circular, o sangue encontra o atrito das paredes arteriais, por isso o coração bate sistematicamente em intervalos regulares. Temos dois tipos de pressão, uma decorrente da força imposta pelo coração e outra imposta pelo calibre arterial. A força realizada pelo coração para impulsionar o sangue é denominada de sistólica (pressão máxima) e a resistência oferecida pelas paredes arteriais ao sangue impulsionado é chamada de diastólica (pressão mínima).
Quando medimos nossa pressão arterial com o aparelho conhecido como esfigmomanômetro, e detectamos, por exemplo, o valor de 11 por 7, estamos sendo informados que nossa pressão máxima é de 110 mmHg (milímetros de mercúrio) e a pressão mínima é de 70 mmHg. O coração impulsiona o sangue a uma força de 110 e a resistência da parede arterial é de 70. Esse valor utilizado como exemplo é considerado como uma pressão sanguínea normal.
A unidade de medida da pressão arterial, dada por mmHg foi criada em 1643 por Evangelista Torricelli, físico e matemático italiano. A medida de 1 mmHg corresponde a 133,32 Pa (Pascal), 1,33 mb (Milibar) e 0,00131578947368 atm (Atmosfera) que são unidades de medidas de pressão de acordo com o SI (Sistema Internacional de Medidas).
A alta da pressão arterial ocorre mediante a diminuição do diâmetro das artérias, pois, nesse caso, o coração deve aumentar a força do batimento para que o sangue atinja todas as partes do corpo. Esse estreitamento das artérias pode ser de origem natural ou devido à alimentação rica em gorduras e sal, que se alojam na parede das artérias próximas ao coração. As bebidas alcoólicas e o cigarro também influenciam no aumento da pressão.
Momento de fé
Havia um professor de filosofia que era um ateu convicto.
Sempre sua meta principal era tomar um semestre inteiro para provar que DEUS não existe.
Os estudantes sempre tinham medo de argüi-lo por causa da sua lógica impecável.
Por 20 anos ensinou e mostrou que jamais haveria alguém que ousasse contrariá-lo, embora, às vezes surgisse alguém que o tentasse, nunca o venciam.
No final de todo semestre, no último dia, fazia a mesma pergunta à sua classe de 300 alunos:
- Se há alguém aqui que ainda acredita em Jesus, que fique de pé!
Em 20 anos ninguém ousou levantar-se.
Sabiam o que o professor faria em seguida. Diria : - Porque qualquer um que acredita em Deus é um tolo! Se Deus existe impediria que este giz caísse ao chão e se quebrasse.
Esta simples questão provaria que Ele existe, mas, não pode fazer isso!
E todos os anos soltava o giz, que caia ao chão partindo-se em pedaços.
E todos os estudantes apenas ficavam quietos,
vendo a DEMONSTRAÇÃO.
A maioria dos alunos pensavam que Deus poderia não existir. Certamente, havia alguns cristãos mas, todos tiveram muito medo de ficar de pé.
Bem.... há alguns anos chegou a vez de um jovem cristão que tinha ouvido sobre a fama daquele professor. O jovem estava com medo, mas, por 3 meses daquele semestre orou todas as manhãs, pedindo que tivesse coragem de se levantar, não importando o que o professor dissesse ou o que a classe pensasse. Nada do que dissessem abalaria sua fé...
ao menos era seu desejo.
Finalmente o dia chegou. O professor disse:
- Se há alguém aqui que ainda acredita em Jesus, que fique de pé!
O professor e os 300 alunos viram, atônitos, o rapaz levantar-se no fundo da sala.
O professor gritou:
- Você é um TOLO!!! Se Deus existe impedirá que este giz caia ao chão e se quebre!
E começou a erguer o braço, quando soltou o giz, escorregou entre seus dedos, deslizou pela camisa, por uma das pernas da calça, correu sobre o sapato e ao tocar no chão simplesmente rolou, sem se quebrar.
O queixo do professor caiu enquanto seu olhar, assustado, seguia o giz.
Quando o giz parou de rolar levantou a cabeça... encarou o jovem e... saiu apressadamente da sala.
O rapaz caminhou firmemente para a frente de seus colegas e, por meia hora, compartilhou sua fé em Jesus. Os 300 estudantes ouviram, silenciosamente, sobre o amor de Deus por todos e sobre seu poder através de Jesus.
Muitas vezes passamos por situações em que acreditamos que "nosso giz" vai quebrar, mas Deus, com sua infinita sabedoria e poder faz o contrário, por isso, você tem duas opões:
1 - Apagar esta mensagem e esquecer a história ou,
2 - Passar a seus amigos, cristãos e não cristãos, dando-lhes a coragem que precisamos todos os dias ao nos levantarmos, e quem sabe a partir de agora você como o professor acredite nesse Deus tão maravilhoso!
EU ESTOU DE PÉ!!! Alguém me acompanha???
"Entender a vontade de Deus para nós, nem sempre é fácil, mas crer que Ele está no comando e que tem um plano pra nossa vida, faz a caminhada valer a pena." Deus te abençoe!
Criado por professor Luciano César
sábado, 10 de julho de 2010
Perfil do aluno em Matemática
MATEMÁTICA DE 4ª SÉRIE
Folha Online, 13/09/2010
Um quinto dos alunos que terminam o ensino médio no Brasil não
sabe em matemática nem o que se espera para um estudante do 5º ano
(ou 4ª série) do fundamental. A informação é da reportagem de
Antônio Gois publicada na edição desta segunda-feira da Folha
(íntegra está disponível para assinantes do jornal e do UOL).
Ainda de acordo com o texto, apenas 11% têm conhecimento adequado
para este nível de ensino na disciplina. No caso dos estudantes
com conhecimento abaixo do 5º ano, isso significa que fazem apenas
operações básicas como soma e divisão. Ao se depararem com
gráficos com mais de uma coluna ou na hora de converter medidas -
como quilogramas em gramas - apresentam dificuldades.
Os dados foram obtidos pela Folha a partir da Prova Brasil e
do Saeb, exames do Ministério da Educação que avaliam alunos de
escolas públicas e particulares em matemática e português. Entre
todos os níveis analisados - a prova avalia alunos no 5º e 9º anos
do fundamental, além da última série do médio -, o pior desempenho
foi em matemática no 3º ano do antigo colegial.\\
Fonte: http://www1.folha.uol.com.br/saber/797838-15-dos-estudantes-brasileiros-sai-do-colegial-com-matematica-de-4-serie.shtml
Transformações trigonométricas
Adição de arcos
Cosseno da soma
Considere a figura ao lado. Sejam três pontos 
 e
e  pertencentes à circunferência , cujas coordenadas são
pertencentes à circunferência , cujas coordenadas são 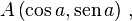
 e
e 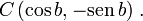 Os arcos
Os arcos 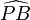 e
e  têm medidas iguais, logo as cordas
têm medidas iguais, logo as cordas  e
e 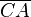 também têm a mesma medida. Após aplicarmos a fórmula da distância entre dois pontos da Geometria analítica, temos:
também têm a mesma medida. Após aplicarmos a fórmula da distância entre dois pontos da Geometria analítica, temos:


Ao igualarmos as duas expressões, temos a fórmula:
Seno da soma
Sabemos que  A partir disto e sendo
A partir disto e sendo 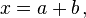 obtemos:
obtemos:
Utilizando a fórmula do cosseno da diferença de dois arcos nessa última expressão:
Substituindo  e
e  nesta expressão, então:
nesta expressão, então:
Tangente da soma
Sabendo que  e utilizando as fórmulas anteriores para soma de senos e cossenos, podemos facilmente conseguir uma expressão para
e utilizando as fórmulas anteriores para soma de senos e cossenos, podemos facilmente conseguir uma expressão para 

Então:
Vale lembrar que essa fórmula só pode ser usada se  e
e  porque a relação
porque a relação  só é válida se e somente se
só é válida se e somente se 
Cotangente da soma
Como  podemos obter, de maneira semelhante à formula da tangente da soma, uma expressão para
podemos obter, de maneira semelhante à formula da tangente da soma, uma expressão para 

Simplificando, temos:
Como  é válida se e somente se
é válida se e somente se  a identidade que demonstramos acima só pode ser usada se
a identidade que demonstramos acima só pode ser usada se  e
e 
Exemplos
- Calcule:
-
- Resolução


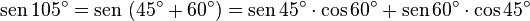







Subtração de arcos
Cosseno da diferença
Para calcular  fazemos uso da igualdade
fazemos uso da igualdade  na fórmula do cosseno da soma, conforme a seguir:
na fórmula do cosseno da soma, conforme a seguir:


Então:
Seno da diferença
Podemos fazer a mesma substituição da igualdade  para encontrar as outras relações de diferença de arcos. Para o seno, usaremos a fórmula do seno da soma e a igualdade citada acima, conforme a seguir:
para encontrar as outras relações de diferença de arcos. Para o seno, usaremos a fórmula do seno da soma e a igualdade citada acima, conforme a seguir:
Logo,
Tangente da diferença
Usando novamente a igualdade  e, desta vez, a fórmula da tangente da soma:
e, desta vez, a fórmula da tangente da soma:
Simplificando, temos:
Pelos motivos já citados anteriormente, esta fórmula só é válida se  e
e 
Cotangente da diferença
Mais uma vez, usaremos a igualdade  e, desta vez, a fórmula da cotangente da soma:
e, desta vez, a fórmula da cotangente da soma:
Logo, obtemos a identidade:
Está fórmula só pode ser aplicada se  e
e 
Exemplos
- Calcule:
-
- Resolução









- Dados
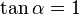 e
e  calcule
calcule 
-
- Resolução


Multiplicação de arcos
É possível deduzir fórmulas para calcular as funções trigonométricas de 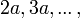 utilizando as fórmulas obtidas para a soma de arcos e fazendo
utilizando as fórmulas obtidas para a soma de arcos e fazendo 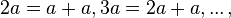 conforme será mostrado adiante.
conforme será mostrado adiante.
Cosseno
Usando a fórmula do cosseno da soma, temos:
Logo, utilizando a Identidade relacional básica, podemos obter duas fórmulas finais:
ou



Utilizando a Identidade relacional básica e trabalhando algebricamente, temos:
Expressões para  são obtidas por processos semelhantes.
são obtidas por processos semelhantes.
Seno
Ultilizando a fórmula do seno da soma:
Então, temos:
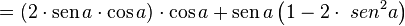
Utilizando a Identidade relacional básica:
Logo:
Expressões para  são obtidas por processos semelhantes.
são obtidas por processos semelhantes.
Tangente
A partir da fórmula da tangente da soma:
Logo:
Ao subtituimos a fórmula anterior para 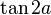 e simplificarmos, obtemos como fórmula final:
e simplificarmos, obtemos como fórmula final:
Expressões para  são obtidas por processos semelhantes.
são obtidas por processos semelhantes.
Exemplo
- Se
 e
e  calcule
calcule 
-
- Resolução
Precisamos encontrar  para aplicarmos a fórmula. Para tanto, utilizaremos a identidade
para aplicarmos a fórmula. Para tanto, utilizaremos a identidade 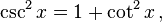 que relaciona as funções cotangente e cossecante. A partir da cossecante obtida, podemos encontrar o valor do seno, uma vez que
que relaciona as funções cotangente e cossecante. A partir da cossecante obtida, podemos encontrar o valor do seno, uma vez que  Como
Como  o valor da cossecante é positivo.
o valor da cossecante é positivo.

De onde vem 
Podemos finalmente calcular:

Bissecção de arcos
Cosseno
Vamos utilizar as duas fórmulas que encontramos para  a fim de que, dado o cosseno de uma arco
a fim de que, dado o cosseno de uma arco  qualquer, possamos obter
qualquer, possamos obter  ou
ou  Para isto, consideraremos
Para isto, consideraremos 
A partir de 
A partir de  temos:
temos:
Finalmente, sabendo que  temos:
temos:
Seno
Caso nos seja dado o  sabendo que
sabendo que  calculamos
calculamos  e usamos as fórmulas dadas logo acima para o cosseno.
e usamos as fórmulas dadas logo acima para o cosseno.
Tangente
Precisamos agora encontrar fórmulas que permitam calcular 
 e
e 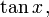 conhecida a
conhecida a  Para tanto, tomaremos as fórmulas de multiplicação
Para tanto, tomaremos as fórmulas de multiplicação


e consideraremos  de modo que:
de modo que:
Exemplos
- Se
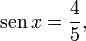 com
com  calcule as funções circulares de
calcule as funções circulares de 
-
- Resolução

Logo, temos:
- Se
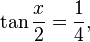 determine
determine 
-
- Resolução
Podemos aplicar diretamente a fórmula, de modo que:

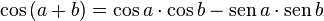
![\mathrm{sen}\, \left ( a + b \right ) = \cos \left [ \frac{\pi}{2} - \left ( a + b \right ) \right ] = \cos \left [ \left ( \frac{\pi}{2} - a \right ) - b \right ]](http://upload.wikimedia.org/math/6/f/e/6fe9329ba5e60e1289e0ce14f545cb3f.png)











![\cos \left ( a - b \right ) = \cos \left [ a + \left ( -b \right ) \right ] \;\!](http://upload.wikimedia.org/math/0/8/b/08bf8219fc6048c78623d4d7368053b4.png)
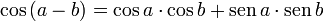
![\mathrm{sen}\, \left ( a - b \right ) = \mathrm{sen}\, \left [ a + \left ( -b \right ) \right ] = \mathrm{sen}\, a\cdot\cos \left ( -b \right ) + \mathrm{sen}\, \left ( -b \right )\cdot\cos a \;\!](http://upload.wikimedia.org/math/0/9/4/0948c83d3bd459b0a8321b2458b0f1b2.png)

![\tan \left ( a - b \right ) = \tan \left [ a + \left ( - b \right ) \right ] = \frac{\tan a + \tan \left ( -b \right )}{1 - \tan a\cdot\tan \left ( -b \right )}](http://upload.wikimedia.org/math/e/a/e/eae9162e77a213f16200443ee63301b9.png)

![\cot \left ( a - b \right ) = \cot \left [ a + \left ( -b \right ) \right ] = \frac{\cot a\cdot\cot \left ( -b \right ) - 1}{\cot a + \cot \left ( -b \right )}](http://upload.wikimedia.org/math/f/2/3/f238db03f70111c90309eddb92193cb8.png)